Impact Gravity
Linear Impact Deflections and Stresses (kinetic loads) [see Budynas p. 191]
Material properties are available is charts (Table 1).  

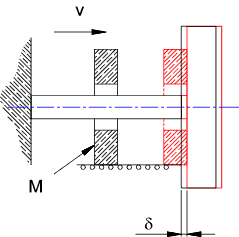
Important note: This calculator represent a very simple view of the loading condition and do not consider a more real case involving shock waves being propagated through the loaded member or the moving mass.

Impact loads based pimarily on kinetic energy e.g horizontal impacts are treated slightly differently. For these applications the kinetic energy is converted into stored energy due to elasticity of the resisting element. Consider a Mass M (lbm) with a velocity of v impacting on a collar which is supported by a bar with a stiffness of K (lbf/in) - Ignoring gravitational forces. The kinetic energy of the mass Mv2/2 is transformed into stored energy in the support.


Max. Deflection Equation: \delta _{max} = \delta_{st}\sqrt{\frac{v^{2}}{g\delta_{st}}} where:\delta_{st} = Wl/AE

Max. Stress Equation:\sigma _{max}=v\sqrt{\frac{ME}{Al}}

Factor of Safety Equation:n=S_{y}/\sigma_{max}
Load Weight (W): Beam Support Area (A): Beam Length (l):
lbf [lbm] in2 in
Beam Elastic Modulus (E): Load Velocity (v): Beam Yield Strength (Sy):
ksi ft/s ksi
Max. Deflection (\delta _{max}): in
Max. Stress: psi
Factor of Safety:

Copyright © 2014 Estiven R. Sierra