Important note: This calculator represent a very simple view of the loading condition and do not consider a more real case involving shock waves being propagated through the loaded member or the moving mass.
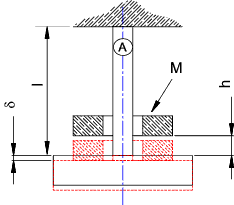
Consider a loading regime as shown below with a ring of Mass M (lbm) with weight W = M.g (lbf) being dropped through a distance h (in) onto a collar supported by a vertical bar which behaves as a spring with a stiffness of k (lbf/in). The support bar has a length l (in), an Area A (in2) with a modulus of elasticity E (ksi).
In practice the weight would impact onto the support which would elastically deform until all of the potential energy has been absorbed. The support would then contract initiating damped oscillations until the system assumes a stable static position. The equations below determine the initial maximum deformation which provides the most highly stressed condition.
Max. Deflection Equation: \delta _{max} = \delta_{st} + \sqrt{(\delta_{st})^{2}+2\delta_{st}h} where:\delta_{st} = Wl/AE
Max. Stress Equation:\sigma _{max}=(k\delta_{max})/A where:k =EA/l
Factor of Safety Equation:n=S_{y}/\sigma_{max}